- …
Excerpts from Algorithms and Data Structures Interview - Deckly by :
Algo Deck

Anki
Check the Anki version here.
Array
Algorithm to reverse an array
int i = 0;
int j = a.length - 1;
while (i < j) {
swap(a, i++, j--);
}Array complexity: access, search, insert, delete
Access: O(1)
Search: O(n)
Insert: O(n)
Delete: O(n)
Binary search in a sorted array algorithm
int lo = 0, hi = a.length - 1;
while (lo <= hi) {
int mid = lo + ((hi - lo) / 2);
if (a[mid] == key) {
return mid;
}
if (a[mid] < key) {
lo = mid + 1;
} else {
hi = mid - 1;
}
}Further Reading
- Nearly All Binary Searches and Mergesorts are Broken by the Google AI Blog
Find an element in a rotated sorted array
Solution: binary search
Check first if the array is rotated. If not, apply normal binary search
If rotated, find pivot (smallest element, only element whose previous is bigger)
Then, check if the element is in 0..pivot-1 or pivot..len-1
int findElementRotatedArray(int[] a, int val) {
// If array not rotated
if (a[0] < a[a.length - 1]) {
// We apply the normal binary search
return binarySearch(a, val, 0, a.length - 1);
}
int pivot = findPivot(a);
if (val >= a[0] && val <= a[pivot - 1]) {
// Element is before the pivot
return binarySearch(a, val, 0, pivot - 1);
} else if (val >= a[pivot] && val < a.length - 1) {
// Element is after the pivot
return binarySearch(a, val, pivot, a.length - 1);
}
return -1;
}Given an array, move all the 0 to the left while maintaining the order of the other elements
Example: 1, 0, 2, 0, 3, 0 => 0, 0, 0, 1, 2, 3
Two pointers technique: read and write starting at the end of the array
If read is on a 0, decrement read. Otherwise swap, decrement both
public void move(int[] a) {
int w = a.length - 1, r = a.length - 1;
while (r >= 0) {
if (a[r] == 0) {
r--;
} else {
swap(a, r--, w--);
}
}
}Time complexity: O(n)
Space complexity: O(1)
How to detect if an element is a pivot in a rotated sorted array
Only element whose previous is bigger (also the pivot is the smallest element)
How to find a pivot element in a rotated array
Check first if the array is rotated
Then, apply binary search (comparison with a[right] to know if we go left or right)
int findPivot(int[] a) {
int left = 0, right = a.length - 1;
// Array is not rotated
if (a[left] < a[right]) {
return -1;
}
while (left <= right) {
int mid = left + ((right - left) / 2);
if (mid > 0 && a[mid] < a[mid - 1]) {
return a[mid];
}
if (a[mid] < a[right]) {
// Pivot is on the left
right = mid - 1;
} else {
// Pivot is on the right
left = mid + 1;
}
}
return -1;
}How to find the duplicates in an array
- Hashtable
- Sorting the array then iterating over each element and check if previous = current
How to manage a dynamic array
When full, create a new array of twice the size, copy items (System.arraycopy is optimized for that)
Shrink: - Not when one-half full (otherwise worst case is too expensive: double-shrink-double-shrink etc.) - Solution: one-quarter full
How to test if the array is sorted in ascending or descending order
Test first and last element (no iteration)
Rotate an array by n elements (n can be negative)
Example: 1, 2, 3, 4, 5 with n = 3 => 3, 4, 5, 1, 2
- Reverse the initial array
- Reverse from 0 to n-1
- Reverse from n to len - 1
void rotateArray(List<Integer> a, int n) {
if (n < 0) {
n = a.size() + n;
}
reverse(a, 0, a.size() - 1);
reverse(a, 0, n - 1);
reverse(a, n, a.size() - 1);
}Time complexity: O(n)
Memory complexity: O(1)
Bit
& operator
AND bit by bit
<< operator
Shift on the left
n * 2 <=> left shift by 1
n * 4 <=> left shift by 2
>> operator
Shift on the right
>>> operator
Logical shift (shift the sign bit as well)
^ operator
XOR bit by bit
Bit vector structure
Vector (linear sequence of numeric values stored contiguously in memory) in which each element is a bit (so either 0 or 1)
Check exactly one bit is set
boolean checkExactlyOneBitSet(int num) {
return num != 0 && (num & (num - 1)) == 0;
}Clear bits from i to 0
int clearBitsFromITo0(int num, int i) {
int mask = (-1 << (i + 1));
return num & mask;
}Clear bits from most significant one to i
int clearBitsFromMsbToI(int num, int i) {
int mask = (1 << i) - 1;
return num & mask;
}Clear ith bit
int clearBit(final int num, final int i) {
final int mask = ~(1 << i);
return num & mask;
}Flip ith bit
int flipBit(final int num, final int i) {
return num ^ (1 << i);
}Get ith bit
boolean getBit(final int num, final int i) {
return ((num & (1 << i)) != 0);
}How to flip one bit
b ^ 1
How to represent signed integers
Use the most significative bit to represent the sign. Yet, it is not enough (problem with this technique: 5 + (-5) != 0)
Two’s complement technique: take the one complement and add one
-3: 1101
-2: 1110
-1: 1111
0: 0000
1: 0001
2: 0010
3: 0011
The most significant bit still represents the sign
Max integer value: 1…1 (31 bits)
-1: 1…1 (32 bits)
Set ith bit
int setBit(final int num, final int i) {
return num | (1 << i);
}Update a bit from a given value
- Clear this bit
- Apply OR on the result with a 0 or 1 left shifted to its index
int updateBit(int num, int i, boolean bit) {
int value = bit ? 1 : 0;
int mask = ~(1 << i);
return (num & mask) | (value << i);
}x & 0s
0
x & 1s
x
x & x
x
x ^ 0s
x
x ^ 1s
~x
x ^ x
0
x | 0s
x
x | 1s
1s
x | x
x
XOR operations
0 ^ 0 = 0
1 ^ 0 = 1
0 ^ 1 = 1
1 ^ 1 = 0
n XOR 0 => keep
n XOR 1 => flip
| operator
OR bit by bit
~ operator
Complement bit by bit
Complexity
0/1 Knapsack brute force complexity
Time complexity: O(2^n) with n the number of items
Space complexity: O(n)
0/1 Knapsack memoization complexity
Time and space complexity: O(n * c) with n the number items and c the capacity
0/1 Knapsack tabulation complexity
Time and space complexity: O(n * c) with n the number of items and c the capacity
Space complexity could even be improved to O(2*c) = O(c) as we need to store only the last 2 lines (using row%2):
int[][] dp = new int[2][c + 1];Amortized complexity definition
How much of a resource (time or memory) it takes to execute per operation on average
Array complexity: access, search, insert, delete
Access: O(1)
Search: O(n)
Insert: O(n)
Delete: O(n)
B-tree complexity: access, insert, delete
All: O(log n)
BFS and DFS graph traversal time and space complexity
Time: O(v + e) with v the number of vertices and e the number of edges
Space: O(v)
BFS and DFS tree traversal time and space complexity
BFS: time O(v), space O(v)
DFS: time O(v), space O(h) (height of the tree)
Big O
Upper bound
Big Omega
Lower bound (fastest)
Big Theta
Theta(n) if both O(n) and Omega(n)
Binary heap (min-heap or max-heap) complexity: insert, get min (max), delete min (max)
Insert: O(log (n))
Get min (max): O(1)
Delete min: O(log n)
If not balanced O(n)
If balanced O(log n)
BST delete algo and complexity
Find inorder successor and swap it
Average: O(log n)
Worst: O(h) if not self-balanced BST, otherwise O(log n)
Bubble sort complexity and stability
Time: O(n²)
Space: O(1)
Stable
Complexity of a function making multiple recursive subcalls
Time: O(branches^depth) with branches the number of times each recursive call branches (english: 2 power 3)
Space: O(depth) to store the call stack
Complexity to create a trie
Time and space: O(n * l) with n the number of words and l the longest word length
Complexity to insert a key in a trie
Time: O(k) with k the size of the key
Space: O(1) iterative, O(k) recursive
Complexity to search for a key in a trie
Time: O(k) with k the size of the key
Space: O(1) iterative or O(k) recursive
Counting sort complexity, stability, use case
Time complexity: O(n + k) // n is the number of elements, k is the range (the maximum element)
Space complexity: O(k)
Stable
Use case: known and small range of possible integers
Doubly linked list complexity: access, insert, delete
Access: O(n)
Insert: O(1)
Delete: O(1)
Hash table complexity: search, insert, delete
All: amortized O(1), worst O(n)
Heapsort complexity, stability, use case
Time: Theta(n log n)
Space: O(1)
Unstable
Use case: space constrained environment with O(n log n) time guarantee
Yet, not stable and not cache friendly
Insertion sort complexity, stability, use case
Time: O(n²)
Space: O(1)
Stable
Use case: partially sorted structure
Linked list complexity: access, insert, delete
Access: O(n)
Insert: O(1)
Delete: O(1)
Mergesort complexity, stability, use case
Time: Theta(n log n)
Space: O(n)
Stable
Use case: good worst case time complexity and stable, good with linked list
Quicksort complexity, stability, use case
Time: best and average O(n log n), worst O(n²) if the array is already sorted in ascending or descending order
Space: O(log n) // In-place sorting algorithm
Not stable
Use case: in practice, quicksort is often faster than merge sort due to better locality (not applicable with linked list so in this case we prefer mergesort)
Radix sort complexity, stability, use case
Time complexity: O(nk) // n is the number of elements, k is the maximum number of digits for a number
Space complexity: O(k)
Stable
Use case: if k < log(n) (for example 1M of elements from 0..1000 as 4 < log(1M))
Recursivity impacts on algorithm complexity
Space impact as each call is added to the call stack
Unless we use tail call recursion
Red-black tree complexity: access, insert, delete
All: O(log n)
Selection sort complexity
Time: Theta(n²)
Space: O(1)
Stack implementations and insert/delete complexity
- Linked list with a pointer on the head
Insert: O(1)
Delete: O(1)
- Array
Insert: O(n), amortized time O(1)
Delete: O(1)
Time complexity to build a binary heap
O(n)
Time and space: O(v + e)
Dynamic Programming
Dynamic programming concept
Break down a problem in smaller parts and store the results of these subproblems so that they only need to be computed once
A DP algorithm will search through all of the possible subproblems (main difference with greedy algorithms)
Based on either: - Memoization (top-down) - Tabulation (bottom-up)
Memoization vs tabulation
Optimization technique to cache previously computed results
Used by dynamic programming algorithms
Memoization: top-down (start with a large, complex problem and break it down into smaller sub-problems)
f(x) {
if (mem[x] is undefined)
mem[x] = f(x-1) + f(x-2)
return mem[x]
}Tabulation: bottom-up (start with the smallest solution and then build up each solution until we arrive at the solution to the initial problem)
tabFib(n) {
mem[0] = 0
mem[1] = 1
for i = 2...n
mem[i] = mem[i-2] + mem[i-1]
return mem[n]
}Encoding
ASCII charset
128 characters
Difference encoding/charset
Charset: set of characters to be used (e.g. ASCII 128 characters)
Encoding: translation of a list of characters in binary
Encoding is used because for all charset we can’t guarantee 1 character = 1 byte
Example: UTF-8 to encode Unicode characters using from 1 byte (english) up to 6 bytes
Unicode charset
Superset of ASCII with 2^21 characters
General
Before finding a solution
-
Make sure to understand the problem by listing: - Inputs - Outputs (what do we search) - Constraints
-
Draw examples
Comparator implementation to order two integers
Ordering, min-heap: (a, b) -> a - b
Reverse ordering, max-heap: (a, b) -> b - a
7 ways: 1. a and b do not overlap 2. a and b overlap, b ends after a 3. a completely overlaps b 4. a and b overlap, a ends after b 5. b completely overlaps a 6. a and b do no overlap 7. a and b are equals
Different ways for two intervals to relate to each other if ordered by start then end
2 different ways: - No overlap - Overlap // Merge intervals (start of the first interval, max of the two ends)
Divide and conquer algorithm paradigm
- Divide: break a given problem into subproblems of same type
- Conquer: recursively solve these subproblems
- Combine: combine the answers to solve the initial problem
Example with merge sort: 1. Split the array into two halves 2. Sort them (recursive call) 3. Merge the two halves
How to name a matrix indexes
Use m[row][col] instead of m[y][x]
If stucked on a problem
- Start with the smallest and easiest problem (e.g. 2 elements) and build a solution for that. Then, add elements and see if we can find a common pattern
- Greedy method
- Traversal technique
In place definition
Mutates an input
P vs NP problems
P (polynomial): set of problems that can be solved reasonably fast (example: multiplication, sorting, etc.)
Complexity is not exponential
NP (non-deterministic polynomial): set of problems where given a solution, we can test is it is a correct one in a reasonable amount of time but finding the solution is not fast (example: a 1M*1M sudoku grid, traveling salesman problem, etc)
NP-complete: hardest problems in the NP set
There are other sets of problems that are not P nor NP as an answer is really hard to prove (example: best move in a chess game)
P = NP means does being able to quickly recognize correct answers means there’s also a quick way to find them?
Solving optimization problems
- Greedy method
- Dynamic programming (memoization or tabulation)
- Branch and bound (minimization problem only)
Stable property
Preserve the original order of elements with equal key
What do to after having designed a solution
Testing on nominal cases then edge cases
Time and space complexity
Graph
A* algorithm
Complete solution to find the shortest path to a target node
Algorithm: - Put initial state in a priority queue - While priority queue is not empty: poll an element and inserts all neighbours - If target is reached, update a min variable
Priority is computed using the evaluation function: f(n) = h + g where h is an heuristic (local cost to visit a node) and g is the cost so far (length of the path so far)
Backedge definition
An edge from a node to itself or to an ancestor
Best-first search algorithm
Greedy solution (non-complete) to find the shortest path to a target node
Algorithm: - Put initial state in a priority queue - While target not reached: poll an element and inserts all neighbours
Priority is computed using the evaluation function: f(n) = h where h is an heuristic (local cost to visit a node)
BFS & DFS graph traversal use cases
BFS: shortest path
DFS: does a path exist, does a cycle exist (memo: D for Does)
DFS stores a single path at a time, requires less memory than BFS (on average but same space complexity)
BFS and DFS graph traversal time and space complexity
Time: O(v + e) with v the number of vertices and e the number of edges
Space: O(v)
Bidirectional search
Run two simultaneous BFS, one from the source, one from the target
Once their searches collide, we found a path
If branching factor of a tree is b and the distance to the target vertex is d, then the normal BFS/DFS searching time complexity would we O(b^d)
Here it is O(b^(d/2))
Connected graph definition
If there is a path between every pair of vertices, the graph is called connected
Otherwise, the graph consists of multiple isolated subgraphs
Difference Best-first search and A* algorithms
Best-first search is a greedy solution: not complete // a solution can be not optimal
A*: complete
Dijkstra algorithm
Input: graph, initial vertex
Output: for each vertex: shortest path and previous node // The previous node is the one we are coming from in the shortest path. To find the shortest path between two nodes, we need to iterate backwards. Example: A -> C => E, D, A
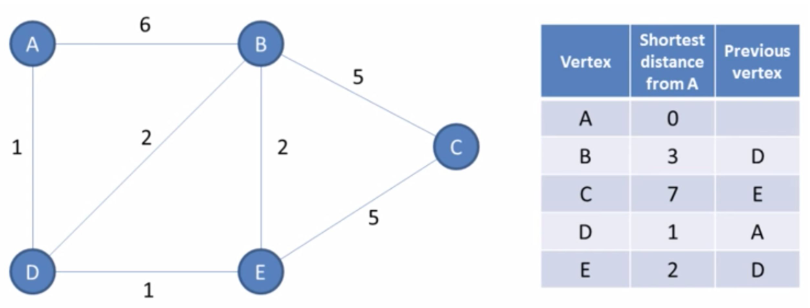
Algorithm: - Init the shortest distance to MAX except for the initial node - Init a priority queue where the comparator will be on the total distance so far - Init a set to store all visited node - Add initial vertex to the priority queue - While queue is not empty: Poll a vertex (mark it visited) and check the total distance to each neighbour (current distance + distance so far), update shortest and previous arrays if smaller. If destination was unvisited, adds it to the queue
void dijkstra(GraphAjdacencyMatrix graph, int initial) {
Set<Integer> visited = new HashSet<>();
int n = graph.vertex;
int[] shortest = new int[n];
int[] previous = new int[n];
for (int i = 0; i < n; i++) {
if (i != initial) {
shortest[i] = Integer.MAX_VALUE;
}
}
// Entry: key=vertex, value=distance so far
PriorityQueue<Entry> minHeap = new PriorityQueue<>((e1, e2) -> e1.value - e2.value);
minHeap.add(new Entry(initial, 0));
while (!minHeap.isEmpty()) {
Entry current = minHeap.poll();
int source = current.key;
int distanceSoFar = current.value;
// Get neighbours
List<GraphAjdacencyMatrix.Edge> edges = graph.getEdge(source);
for (GraphAjdacencyMatrix.Edge edge : edges) {
// For each neighbour, check the total distance
int distance = distanceSoFar + edge.distance;
if (distance < shortest[edge.destination]) {
shortest[edge.destination] = distance;
previous[edge.destination] = source;
}
// Add the element in the queue if not visited
if (!visited.contains(edge.destination)) {
minHeap.add(new Entry(edge.destination, distance));
}
}
visited.add(source);
}
print(shortest);
print(previous);
}Dynamic connectivity problem
Given a set of nodes and edges: are two nodes connected (directly or in-directly)?
Two methods: - union(2, 5) // connect object 2 with object 5 - connected(1 , 6) // is object 1 connected to object 6?
Further Reading
- Dynamic Connectivity Problem by Omar El Gabry
Dynamic connectivity problem - Quick-find solution
Array of integer of size N initialized with their index (0: 0, 1: 1 etc.).
If two indexes have the same value, they belong to the same group.
- Is connected: id[p] == id[q] // O(1)
- Union: change all elements in the array whose value is equals to id[q] and set them to id[p] // O(n)
Dynamic connectivity problem - Quick-union solution
Init: integer array of size N
Interpretation: id[i] is parent of i, root parent if id[i] == i
- Is connected: check if p and q have the same parent // O(n)
- Union: set the id of p’s root to the id of q’s root // O(n)
Dynamic connectivity problem - Weighted Quick-union solution
Modify quick-union to avoid tall tree
Keep track of the size of each tree (number of nodes): extra array size[i] to count number of objects in the tree rooted at i
O(n) extra space
- Union: link root of smaller tree to root of larger tree // O(log(n))
- Is connected: root(p) == root(q) // O(log(n))
Given n tasks from 0 to n-1 and a list of relations so that a -> b means a must be scheduled before b, how to know if it is possible to schedule all the tasks (no cycle)
Solution: topological sort
If there’s a cycle in the relations, it means it is not possible to shedule all the tasks
There is a cycle if the produced sorted array size is different from n
Graph definition
A way to represent a network, or a collection of inteconnected objects
G = (V, E) with V a set of vertices (or nodes) and E a set of edges (or links)
Graph traversal: BFS
Traverse broad into the graph by visiting the sibling/neighbor before children nodes (one level of children at a time)
Iterative using a queue
Algorithm: similar with tree except we need to mark the visited nodes, can start with any nodes
Queue<Node> queue = new LinkedList<>();
Node first = graph.nodes.get(0);
queue.add(first);
first.markVisitied();
while (!queue.isEmpty()) {
Node node = queue.poll();
System.out.println(node.name);
for (Edge edge : node.connections) {
if (!edge.end.visited) {
queue.add(edge.end);
edge.end.markVisited();
}
}
}Graph traversal: DFS
Traverse deep into the graph by visiting the children before sibling/neighbor nodes (traverse down one single path)
Walk through a path, backtrack until we found a new path
Algorithm: recursive or iterative using a stack (same algo than BFS except we use a queue instead of a stack)
How to compute the shortest path between two nodes in an unweighted graph
BFS traversal by using an array to keep track of the min distance distances[i] gives the shortest distance between the input node and the node of id i
Algorithm: no need to keep track of the visited node, it is replaced by a test on the distance array
Queue<Node> queue = new LinkedList<>();
queue.add(parent);
int[] distances = new int[graph.nodes.size()];
Arrays.fill(distances, -1);
distances[parent.id] = 0;
while (!queue.isEmpty()) {
Node node = queue.poll();
for (Edge edge : node.connections) {
if (distances[edge.end.id] == -1) {
queue.add(edge.end);
distances[edge.end.id] = distances[node.id] + 1;
}
}
}How to detect a cycle in a directed graph
Using DFS by marking the visited nodes, there is a cycle if a visited node is also part of the current stack
The stack can be managed as a boolean array
boolean isCyclic(DirectedGraph g) {
boolean[] visited = new boolean[g.size()];
boolean[] stack = new boolean[g.size()];
for (int i = 0; i < g.size(); i++) {
if (isCyclic(g, i, visited, stack)) {
return true;
}
}
return false;
}
boolean isCyclic(DirectedGraph g, int node, boolean[] visited, boolean[] stack) {
if (stack[node]) {
return true;
}
if (visited[node]) {
return false;
}
stack[node] = true;
visited[node] = true;
List<DirectedGraph.Edge> edges = g.getEdges(node);
for (DirectedGraph.Edge edge : edges) {
int destination = edge.destination;
if (isCyclic(g, destination, visited, stack)) {
return true;
}
}
// Backtrack
stack[node] = false;
return false;
}How to detect a cycle in an undirected graph
Using DFS
Idea: for every visited vertex v, if there is an adjacent u such that u is already visited and u is not the parent of v, then there is a cycle
public boolean isCyclic(UndirectedGraph g) {
boolean[] visited = new boolean[g.size()];
for (int i = 0; i < g.size(); i++) {
if (!visited[i]) {
if (isCyclic(g, i, visited, -1)) {
return true;
}
}
}
return false;
}
private boolean isCyclic(UndirectedGraph g, int v, boolean[] visited, int parent) {
visited[v] = true;
List<UndirectedGraph.Edge> edges = g.getEdges(v);
for (UndirectedGraph.Edge edge : edges) {
if (!visited[edge.destination]) {
if (isCyclic(g, edge.destination, visited, v)) {
return true;
}
} else if (edge.destination != parent) {
return true;
}
}
return false;
}How to name a graph with directed edges and without cycle
Directed Acyclic Graph (DAG)
How to name a graph with few edges and with many edges
Sparse: few edges
Dense: many edges
How to name the number of edges
Degree of a vertex
How to represent the edges of a graph (structure and complexity)
- Using an adjacency matrix: two-dimensional array of boolean with a[i][j] is true if there is an edge between node i and j
- Time complexity: O(1)
- Space complexity: O(v²) with v the number of vertices
Problem: - If graph is undirected: half of the space is useless - If graph is sparse, we still have to consume O(v²) space
- Using an adjacency list: array (or map) of linked list with a[i] represents the edges for the node i
- Time complexity: O(d) with d the degree of a vertex
- Space complexity: O(2*e) with e the number of edges
Topological sort complexity
Time and space: O(v + e)
Topological sort technique
If there is an edge from U to V, then U <= V
Possible only if the graph is a DAG
Algo: - Create a graph representation (adjacency list) and an in degree counter (Map) - Zero them for each vertex - Fill the adjacency list and the in degree counter for each edge - Add in a queue each vertex whose in degree count is 0 (source vertex with no parent) - While the queue is not empty, poll a vertex from it then decrement the in degree of its children (no removal)
To check if there is a cycle, we must compare the size of the produced array to the number of vertices
List<Integer> sort(int vertices, int[][] edges) {
if (vertices == 0) {
return Collections.EMPTY_LIST;
}
List<Integer> sorted = new ArrayList<>(vertices);
// Adjacency list graph
Map<Integer, List<Integer>> graph = new HashMap<>();
// Count of incoming edges for each vertex
Map<Integer, Integer> inDegree = new HashMap<>();
for (int i = 0; i < vertices; i++) {
inDegree.put(i, 0);
graph.put(i, new LinkedList<>());
}
// Init graph and inDegree
for (int[] edge : edges) {
int parent = edge[0];
int child = edge[1];
graph.get(parent).add(child);
inDegree.put(child, inDegree.get(child) + 1);
}
// Create a source queue and add each source (a vertex whose inDegree count is 0)
Queue<Integer> sources = new LinkedList<>();
for (Map.Entry<Integer, Integer> entry : inDegree.entrySet()) {
if (entry.getValue() == 0) {
sources.add(entry.getKey());
}
}
while (!sources.isEmpty()) {
int vertex = sources.poll();
sorted.add(vertex);
// For each vertex, we will decrease the inDegree count of its children
List<Integer> children = graph.get(vertex);
for (int child : children) {
inDegree.put(child, inDegree.get(child) - 1);
if (inDegree.get(child) == 0) {
sources.add(child);
}
}
}
// Topological sort is not possible as the graph has a cycle
if (sorted.size() != vertices) {
return new ArrayList<>();
}
return sorted;
}Travelling salesman problem
Find the shortest possible route that visits every city (vertex) exactly once
Possible solutions: - Greedy: nearest neighbour - Dynamic programming: compute optimal solution for a path of length n by using information already known for partial tours of length n-1 (time complexity: n^2 * 2^n)
Two types of graphs
Directed graph (with directed edges)
Undirected graph (with undirected edges)
Greedy
Best-first search algorithm
Greedy solution (non-complete) to find the shortest path to a target node
Algorithm: - Put initial state in a priority queue - While target not reached: poll an element and inserts all neighbours
Priority is computed using the evaluation function: f(n) = h where h is an heuristic (local cost to visit a node)
Greedy algorithm
Algorithm paradigm of making the locally optimal choice at each stage using a heuristic function
A locally optimal function does not necesseraly mean to not have a global context for taking a decision
Never reconsider a choice (main difference with dynamic programming)
Solution found may not be the most optimal one
Greedy algorithm: structure
Often, the global context is spread into a priority queue
Greedy technique
Identify an optimal subproblem or substructure in the problem and determine how to reach it
Focus on what you have now (don’t think about what comes next)
We may want to apply the traversal technique to have a global context for the identification part (a map of letters/positions etc.)
Technique - Optimization problems requiring a min or max
Greedy technique
Hash Table
Hash table complexity: search, insert, delete
All: amortized O(1), worst O(n)
Hash table implementation
- Array of linked list
- Hash code function to give the array index
Resize the array when a threshold is reached
If extreme nonuniform distribution, could be replaced by array of BST
Heap
Binary heap (min-heap or max-heap) complexity: insert, get min (max), delete min (max)
Insert: O(log (n))
Get min (max): O(1)
Delete min: O(log n)
Binary heap (min-heap or max-heap) data structure used for the implementation
Using an array
If children at index i: - Left children: 2 * i + 1 - Right children: 2 * i + 2 - Parent: (i - 1) / 2
Binary heap (min-heap or max-heap) definition
A binary heap is a a complete binary tree with min-heap or max-heap property ordering. Also called min heap or max heap.
Min heap: each node smaller than its children, min value element at the root.
Two operations: insert(), getMin()
Difference BST: in a BST, each smaller element is on the left and greater element on the right, here a smaller element can be found on the left or the right side.
Binary heap (min-heap or max-heap) delete min
Replace min element (root) with the last node (left-most, lowest-level node because a binary heap is a complete binary tree)
If violations, swap with the smallest child (level by level)
Binary heap (min-heap or max-heap) insert algorithm
Insert node at the end (left-most spot because a binary heap is a complete binary tree)
If violations, swap with parents until no more violation
Binary heap (min-heap or max-heap) use-cases
Priority queue
Comparator implementation to order two integers
Ordering, min-heap: (a, b) -> a - b
Reverse ordering, max-heap: (a, b) -> b - a
Convert an array into a binary heap in place
For i from 0 to n-1, swap recursively element a[i] until min/max heap violation on its node
Find the median of a stream of numbers, 2 methods insert(int) and int findMedian()
Solution: two heap technique
Keep two heaps and maintain the balance by transfering an element from one heap to another if not balanced
Return the median (difference if even or odd)
// First half
PriorityQueue<Integer> maxHeap = new PriorityQueue<>((a, b) -> b - a);
// Second half
PriorityQueue<Integer> minHeap = new PriorityQueue<>();
public void insertNum(int n) {
// First element
if (minHeap.isEmpty()) {
minHeap.add(n);
return;
}
// Insert into min or max heap
Integer minSecondHalf = minHeap.peek();
if (n >= minSecondHalf) {
minHeap.add(n);
} else {
maxHeap.add(n);
}
// Is balanced?
if (minHeap.size() > maxHeap.size() + 1) {
maxHeap.add(minHeap.poll());
} else if (maxHeap.size() > minHeap.size() + 1) {
minHeap.add(maxHeap.poll());
}
}
public double findMedian() {
// Even
if (minHeap.size() == maxHeap.size()) {
return (double) (minHeap.peek() + maxHeap.peek()) / 2;
}
// Odd
if (minHeap.size() > maxHeap.size()) {
return minHeap.peek();
}
return maxHeap.peek();
}Given an unsorted array of numbers, find the K largest numbers in it
Solution: using a min heap but we keep only K elements in it
public static List<Integer> findKLargestNumbers(int[] nums, int k) {
PriorityQueue<Integer> minHeap = new PriorityQueue<>();
// Put the first K numbers
for (int i = 0; i < k; i++) {
minHeap.add(nums[i]);
}
// Iterate on the rest of the array
// Check whether the current element is bigger than the smallest one
for (int i = k; i < nums.length; i++) {
if (nums[i] > minHeap.peek()) {
minHeap.poll();
minHeap.add(nums[i]);
}
}
return toList(minHeap);
}
public static List<Integer> toList(PriorityQueue<Integer> minHeap) {
List<Integer> list = new ArrayList<>(minHeap.size());
while (!minHeap.isEmpty()) {
list.add(minHeap.poll());
}
return list;
}Space complexity: O(k)
Heapsort algorithm
- Build a max heap from the array
- For i from n-1 to 0:
- Swap the largest element (at index 0) with i
- Heapify the remaining elements (0.. i -1) by putting the root element at its correct position (keep swapping element with biggest child until there is a max heap violation on a node)
Is binary heap stable?
Stable
Time complexity to build a binary heap
O(n)
Two heaps technique
Keep two heaps: - A max heap for the first half - Then a min heap for the second half
May be required to balance them to have at most a difference in terms of size of 1
Why binary heap over BST for priority queue?
BST needs an extra pointer to the min or max value (otherwise finding the min or max is O(log n))
Implemented using an array: faster in practice (better locality, more cache friendly)
Building a binary heap is O(n), instead of O(n log n) for a BST
Linked List
Algorithm to reverse a linked list
public ListNode reverse(ListNode head) {
ListNode previous = null;
ListNode current = head;
while (current != null) {
// Keep temporary next node
ListNode next = current.next;
// Change link
current.next = previous;
// Move previous and current
previous = current;
current = next;
}
return previous;
}Doubly linked list
Each node contains a pointer to the previous and the next node
Doubly linked list complexity: access, insert, delete
Access: O(n)
Insert: O(1)
Delete: O(1)
Get the middle of a linked list
Using the runner technique
Iterate over two linked lists
while (l1 != null || l2 != null) {
}Linked list complexity: access, insert, delete
Access: O(n)
Insert: O(1)
Delete: O(1)
Linked list questions prerequisite
Single or doubly linked list?
Queue implementations and insert/delete complexity
- Linked list with pointers on head and tail
Insert: O(1)
Delete: O(1)
- Circular buffer if queue has a fixed size using a read and write pointer
Insert: O(1)
Delete: O(1)
Ring buffer (or circular buffer) structure
Data structure using a single, fixed-sized buffer as if it were connected end-to-end
What if we need to iterate backwards on a singly linked list in constant space without mutating the input?
Reverse the liked list (or a subpart only), implement the algo then reverse it again to the initial state
Math
a = a property
Reflexive
If a = b and b = c then a = c property
Transitive
If a = b then b = a property
Symmetric
Logarithm definition
Inverse function to exponentiation
- log2(1) = 0
- log2(2) = 1
- log2(4) = 2
- log2(8) = 3
- log2(16) = 4
- etc.
Median of a sorted array
If odd: middle value
If even: average of the two middle values (1, 2, 3, 4 => (2 + 3) / 2 = 2.5)
n-choose-k problems
From a set of n items, choose k items with 0 <= k <= n
P(n, k)
Order matters: n! / (n - k)! // How many permutations
Order does not matter: n! / ((n - k)! k!) // How many combinations
Probability: P(a ∩ b) // inter
P(a ∩ b) = P(a) * P(b)
Probability: P(a ∪ b) // union
P(a ∪ b) = P(a) + P(b) - P(a ∩ b)
Probability: Pb(a) // probability of a knowing b
Pb(a) = P(a ∩ b) / P(b)
Queue
Dequeue data structure
Double ended queue for which elements can be added or removed from either the front (head) or the back (tail)
Queue
FIFO (First In First Out)
Queue implementations and insert/delete complexity
- Linked list with pointers on head and tail
Insert: O(1)
Delete: O(1)
- Circular buffer if queue has a fixed size using a read and write pointer
Insert: O(1)
Delete: O(1)
Recursion
How to handle a recursive function that need to return a list
Input: - Result List - Current iteration element
Output: void
void f(List<String> result, String current) {
// Do something
result.add(...);
}How to handle a recursive function that need to return a maximum value
Implementation: return max(f(a), f(b))
Loop inside of a recursive function?
Might be a code smell. The iteration is already brought by the recursion itself.
Sort
Bubble sort algorithm
Walk through a collection and compares 2 elements at a time
If they are out of order, swap them
Continue until the entire collection is sorted
Bubble sort complexity and stability
Time: O(n²)
Space: O(1)
Stable
Counting sort complexity, stability, use case
Time complexity: O(n + k) // n is the number of elements, k is the range (the maximum element)
Space complexity: O(k)
Stable
Use case: known and small range of possible integers
Counting sort algorithm
If range r is known
-
Create an array of size r where each a[i] represents the number of occurences of i
-
Modify the array to store the cumulative sum (if a=[1, 3, 0, 2] => [1, 4, 4, 6])
-
Right shift the array with a backward iteration (element at index 0 is 0 => [0, 1, 4, 4]) Now a[i] represents the first index of i if array was sorted
-
Create the sorted array by filling the elements from their first index
Heapsort algorithm
- Build a max heap from the array
- For i from n-1 to 0:
- Swap the largest element (at index 0) with i
- Heapify the remaining elements (0.. i -1) by putting the root element at its correct position (keep swapping element with biggest child until there is a max heap violation on a node)
Heapsort complexity, stability, use case
Time: Theta(n log n)
Space: O(1)
Unstable
Use case: space constrained environment with O(n log n) time guarantee
Yet, not stable and not cache friendly
Insertion sort algorithm
From i to 0..n, insert a[i] to its correct position to the left (0..i)
Used by humans
Insertion sort complexity, stability, use case
Time: O(n²)
Space: O(1)
Stable
Use case: partially sorted structure
Mergesort algorithm
Splits a collection into 2 halves, sort the 2 halves (recursive call) then merge them together to form one sorted collection
void mergeSort(int[] a) {
int[] helper = new int[a.length];
mergeSort(a, helper, 0, a.length - 1);
}
void mergeSort(int a[], int helper[], int lo, int hi) {
if (lo < hi) {
int mid = (lo + hi) / 2;
mergeSort(a, helper, lo, mid);
mergeSort(a, helper, mid + 1, hi);
merge(a, helper, lo, mid, hi);
}
}
private void merge(int[] a, int[] helper, int lo, int mid, int hi) {
// Copy into helper
for (int i = lo; i <= hi; i++) {
helper[i] = a[i];
}
int p1 = lo; // Pointer on the first half
int p2 = mid + 1; // Pointer on the second half
int index = lo; // Index of a
// Copy the smallest values from either the left or the right side back to the original array
while (p1 <= mid && p2 <= hi) {
if (helper[p1] <= helper[p2]) {
a[index] = helper[p1];
p1++;
} else {
a[index] = helper[p2];
p2++;
}
index++;
}
// Copy the eventual rest of the left side of the array into the target array
while (p1 <= mid) {
a[index] = helper[p1];
index++;
p1++;
}
}Further Reading
- Making Sense of Merge Sort - Part 1 by Vaidehi Joshi
- Making Sense of Merge Sort - Part 2 by Vaidehi Joshi
Mergesort complexity, stability, use case
Time: Theta(n log n)
Space: O(n)
Stable
Use case: good worst case time complexity and stable, good with linked list
Quicksort algorithm
Sort a collection by repeatedly choosing a pivot and partitioning the collection around it (smaller before, larger after)
Here the pivot will be the last element of the subarray
In an ideal world, the pivot would be the middle element so that we partition the array in two subsets of equal size
The worst case is to find a pivot element at the top left or top right index of the subarray
void quickSort(int[] a) {
quickSort(a, 0, a.length - 1);
}
void quickSort(int a[], int lo, int hi) {
if (lo < hi) {
int pivot = partition(a, lo, hi);
quickSort(a, lo, pivot - 1);
quickSort(a, pivot + 1, hi);
}
}
// Returns an index so that all element before that index are smaller
// And all element after are bigger
int partition(int a[], int lo, int hi) {
int pivot = a[hi];
int pivotIndex = lo; // Will represent the pivot index
// Iterate using the two pointers technique
for (int i = lo; i < hi; i++) {
// If the current index is smaller, swap and increment pivot index
if (a[i] <= pivot) {
swap(a, pivotIndex++, i);
}
}
swap(a, pivotIndex, hi);
return pivotIndex;
}Quicksort complexity, stability, use case
Time: best and average O(n log n), worst O(n²) if the array is already sorted in ascending or descending order
Space: O(log n) // In-place sorting algorithm
Not stable
Use case: in practice, quicksort is often faster than merge sort due to better locality (not applicable with linked list so in this case we prefer mergesort)
Radix sort algorithm
Sort by applying counting sort on one digit at a time (least to most significant) Each new level must be stable (if equals, keep the order of the previous level)
Example:
- 53, 89, 150, 36, 633, 233
- Counting sort on digit 0 => 150, 53, 633, 36, 89
- Counting sort on digit 1 => 633, 233, 36, 150, 53, 89
- Counting sort on digit 2 => 36, 53, 89, 150, 233, 633 // If does not exist (like 36) it is replaced by 0
Radix sort complexity, stability, use case
Time complexity: O(nk) // n is the number of elements, k is the maximum number of digits for a number
Space complexity: O(k)
Stable
Use case: if k < log(n) (for example 1M of elements from 0..1000 as 4 < log(1M))
Selection sort algorithm
From i to 0..n, find repeatedly the min element then swap it with i
Selection sort complexity
Time: Theta(n²)
Space: O(1)
Shuffling an array
Fisher-Yates shuffle algorithm: - Iterate over each element (i) - Pick a random index (from 0 to i included) and swap with the current element
Stack
Stack
LIFO (Last In First Out)
Stack implementations and insert/delete complexity
- Linked list with a pointer on the head
Insert: O(1)
Delete: O(1)
- Array
Insert: O(n), amortized time O(1)
Delete: O(1)
String
First check to test if two strings are a permutation or a rotation of each other
Same length
How to print all the possible permutations of a string
Recursion with backtracking
void permute(String s) {
permute(s, 0);
}
void permute(String s, int index) {
if (index == s.length() - 1) {
System.out.println(s);
return;
}
for (int i = index; i < s.length(); i++) {
s = swap(s, index, i);
permute(s, index + 1);
s = swap(s, index, i);
}
}Rabin-Karp substring search
Searching a substring s in a string b takes O(s(b-s)) time
Trick: compute the hash of each substring s
Sliding window of size s
Time complexity: O(b)
If hash matches, check if the string are equals (as two different strings can have the same hash)
String permutation vs rotation
Permutation: contains the same characters in an order that can be different (abdc and dabc)
Rotation: rotates according to a pivot
String questions prerequisite
Case sensitive?
Encoding?
Technique
14 Patterns to Ace Any Coding Interview Question by Fahim ul Haq
0/1 Knapsack brute force technique
Recursive approach: solve f(c, i) with c is the remaining capacity and i is th current item index At each level, we branch with the item at index i (if enough capacity) and without it
public int knapsack(int[] profits, int[] weights, int c) {
return knapsack(profits, weights, c, 0, 0);
}
public int knapsack(int[] profits, int[] weights, int c, int i, int sum) {
if (i == profits.length || c <= 0) {
return sum;
}
// Not
int sum1 = knapsack(profits, weights, c, i + 1, sum);
// With
int sum2 = 0;
if (weights[i] <= c) {
sum2 = knapsack(profits, weights, c - weights[i], i + 1, sum + profits[i]);
}
return Math.max(sum1, sum2);
}0/1 Knapsack memoization technique
Memoization: store a[c][i] (c is the remaining capacity, i is the current item index)
As we need to store the 0 capacity, we have to init the array this way:
int[][] a = new int[c + 1][n] // n is the number of items
Time and space complexity: O(n * c)
public int knapsack(int[] profits, int[] weights, int capacity) {
// Capacity from 1 to n
Integer[][] a = new Integer[capacity][profits.length];
return knapsack(profits, weights, capacity, 0, 0, a);
}
public int knapsack(int[] profits, int[] weights, int capacity, int i, int sum, Integer[][] a) {
if (i == profits.length || capacity == 0) {
return sum;
}
// If value already exists, return
if (a[capacity - 1][i] != null) {
return a[capacity][i];
}
// With
int sum1 = knapsack(profits, weights, capacity, i + 1, sum, a);
// Without
int sum2 = 0;
if (weights[i] <= capacity) {
sum2 = knapsack(profits, weights, capacity - weights[i], i + 1, sum + profits[i], a);
}
a[capacity - 1][i] = Math.max(sum1, sum2);
return a[capacity - 1][i];
}0/1 Knapsack tabulation technique
Two dimensional array: a[n + 1][c + 1] // n the number of items and c the max capacity
First row and first column are set to 0
a[row][col] represent the max profit with items 1..row at capacity col
remainingWeight = col - itemWeight // col: current max capacity
a[row][col] = max(a[row - 1][col], itemValue + a[row - 1][remainingWeight]) // max between item not selected and item selected + max remaining weight
If remainingWeight < 0, we can’t chose the item so a[row][col] = a[row - 1][col]
Return last element of the array
public int solveKnapsack(int[] profits, int[] weights, int capacity) {
int[][] a = new int[profits.length + 1][capacity + 1];
for (int row = 1; row < profits.length + 1; row++) {
int value = profits[row - 1];
int weight = weights[row - 1];
for (int col = 1; col < capacity + 1; col++) {
int remainingWeight = col - weight;
if (remainingWeight < 0) {
a[row][col] = a[row - 1][col];
} else {
a[row][col] = Math.max(
a[row - 1][col],
value + a[row - 1][remainingWeight]
);
}
}
}
return a[profits.length][capacity];
}If we need to compute a result like “determine if a subset exists” that return a boolean, the array type is boolean[][]
As we are only interested in the previous row, we can also use an int[2][n] array
Backtracking technique
Solution for solving a problem recursively
Loop: - apply() // Apply a change - try() // Try a solution - reverse() // Reverse apply
Cyclic sort technique
Iterate over each number of an array and swap it to its correct position
At the end, we may iterate on the array to check which number is not at its correct position
If numbers are not within the 1 to n range, we can simply drop them
Alternative: marker technique (mark a result by setting a[i] to negative for example)
Greedy technique
Identify an optimal subproblem or substructure in the problem and determine how to reach it
Focus on what you have now (don’t think about what comes next)
We may want to apply the traversal technique to have a global context for the identification part (a map of letters/positions etc.)
K-way merge technique
Given K sorted array, technique to perform a sorted traversal of all the elements of all arrays
- First, push the first element of each array in a min heap
- While min heap not empty, take min element and push the next element of the same array
We need to keep track of which structure the min element come from (tracking the array index or taking the next node if it’s a linked list)
Runner technique
Iterate over the linked list with two pointers simultaneously either with: - One ahead by a fixed amount - One faster
This technique can also be applied on other problems where we need to find a cycle (f(slow) and f(f(fast)) may converge)
Simplification technique
Simplify the problem. If solvable, generalize to the initial problem.
Example: sort the array first
Sliding window technique
Range of elements in a specific window size
Two pointers left and right: - Move right while condition is valid - Move left if condition is not valid
Subsets technique
Technique to find all the possible permutations or combinations
Start with an empty set, for each element of the input, add them to all the existing subsets to create new subsets
Example: - Given [1, 5, 3] - => [] // Start - => [], [1] - => [], [1], [5], [1,5] - => [], [1], [5], [1,5], [3], [1,3], [1,5,3]
For each level, we iterate from 0 to size // size is the fixed size of the list
List<List<Integer>> findSubsets(int[] a) {
List<List<Integer>> subsets = new ArrayList<>();
// Add subset []
subsets.add(new ArrayList<>());
for (int n : a) {
// Fix the current size
int size = subsets.size();
for (int i = 0; i < size; i++) {
// Copy subset
ArrayList<Integer> newSubset = new ArrayList<>(subsets.get(i));
// Add element
newSubset.add(n);
subsets.add(newSubset);
}
}
return subsets;
}Technique - Dealing with cycles in a linked list or an array
Runner technique
Technique - Find all the permutations or combinations
Subsets technique or recursion + backtracking
Technique - Find an element in a sorted array or linked list
Binary search
Technique - Find or calculate something among all the contiguous subarrays of a given size
Sliding window technique
Example: - Given an array, find the average of all subarrays of size ‘K’ in it
Technique - Find the longest/shortest substring or subarray
Sliding window technique
Example: - Longest substring with K distinct characters - Longest substring without repeating characters
Technique - Find the smallest/largest/median element of a set
Two heaps technique
Technique - Finding a certain element in a linked list (e.g. middle)
Runner technique
Technique - Given a sorted array, find a set of elements that fullfill certain conditions
Two pointers technique
Example: - Given a sorted array and a target sum, find a pair in the array whose sum is equal to the given target - Given an array of unsorted numbers, find all unique triplets in it that add up to zero - Comparing strings containing backspaces
Technique - Given an array of size n containing integer from 1 to n (e.g. with one duplicate)
Cyclic sort technique
Technique - Given time intervals
Traversal technique
Iterate with two pointers, one over the starts, another one over the ends
Handle the element with the lowest value first and generate an event
Example: how many rooms for n meetings => meeting started, meeting started, meeting ended etc.
Technique - How to get the K biggest/smallest/frequent elements
Top K elements technique
Technique - Optimization problems requiring a min or max
Greedy technique
Technique - Problems featuring a list of sorted arrays (merge or find the smallest element)
K-way merge technique
Technique - Scheduling problem with n tasks where each task can have constraints to be completed before others
Topological sort technique
Technique - Situations like priority queue or scheduling
Heap data structure
Possibly two heaps technique
Top K elements technique (biggest and smallest)
Finding the K biggest elements: - Min heap - Add k elements - Then iterate over the remaining elements, if current > min => remove min, add current
Finding the k smallest elements: - Max heap - Add k elements - Then iterate over the remaining elements, if current < max => remove max, add current
Topological sort technique
If there is an edge from U to V, then U <= V
Possible only if the graph is a DAG
Algo: - Create a graph representation (adjacency list) and an in degree counter (Map) - Zero them for each vertex - Fill the adjacency list and the in degree counter for each edge - Add in a queue each vertex whose in degree count is 0 (source vertex with no parent) - While the queue is not empty, poll a vertex from it then decrement the in degree of its children (no removal)
To check if there is a cycle, we must compare the size of the produced array to the number of vertices
List<Integer> sort(int vertices, int[][] edges) {
if (vertices == 0) {
return Collections.EMPTY_LIST;
}
List<Integer> sorted = new ArrayList<>(vertices);
// Adjacency list graph
Map<Integer, List<Integer>> graph = new HashMap<>();
// Count of incoming edges for each vertex
Map<Integer, Integer> inDegree = new HashMap<>();
for (int i = 0; i < vertices; i++) {
inDegree.put(i, 0);
graph.put(i, new LinkedList<>());
}
// Init graph and inDegree
for (int[] edge : edges) {
int parent = edge[0];
int child = edge[1];
graph.get(parent).add(child);
inDegree.put(child, inDegree.get(child) + 1);
}
// Create a source queue and add each source (a vertex whose inDegree count is 0)
Queue<Integer> sources = new LinkedList<>();
for (Map.Entry<Integer, Integer> entry : inDegree.entrySet()) {
if (entry.getValue() == 0) {
sources.add(entry.getKey());
}
}
while (!sources.isEmpty()) {
int vertex = sources.poll();
sorted.add(vertex);
// For each vertex, we will decrease the inDegree count of its children
List<Integer> children = graph.get(vertex);
for (int child : children) {
inDegree.put(child, inDegree.get(child) - 1);
if (inDegree.get(child) == 0) {
sources.add(child);
}
}
}
// Topological sort is not possible as the graph has a cycle
if (sorted.size() != vertices) {
return new ArrayList<>();
}
return sorted;
}Traversal technique
Traverse the input and generate another data structure or optional events
Start the problem from this new state
Two heaps technique
Keep two heaps: - A max heap for the first half - Then a min heap for the second half
May be required to balance them to have at most a difference in terms of size of 1
Two pointers technique
Two pointers iterating through the data structure in tandem until one or both pointers hit a certain condition
Often useful when structure is sorted. If not sorted, we may want to sort it first.
Most of the times (not always): first pointer is at the start, the second pointer is at the end
The two pointers can also be on two different ds, still iterating in tandem (e.g. comparing strings containing backspaces)
Time complexity is linear
What if we need to iterate backwards on a singly linked list in constant space without mutating the input?
Reverse the liked list (or a subpart only), implement the algo then reverse it again to the initial state
Tree
2-3 tree
Self-balanced BST => O(log n) complexity
Either: - 2-node: contains a single value and has two children - 3-node: contains two values and has three children - Leaf: 1 or 2 keys
Insert: find proper leaf and insert the value in-place. If the leaf has 3 values (called temporary 4-node), split the node into three 2-node and insert the middle value into the parent.
AVL tree
If tree is not balanced, rearange the nodes with single or double rotations
B-tree complexity: access, insert, delete
All: O(log n)
B-tree: definition and use case
Self-balanced BST => O(log n) complexity
Can have more than two children (generalization of 2-3 tree)
Use-case: huge amount of data that cannot fit in main memory but disk space.
Height is kept low to reduce the disk accesses.
Match how page disk are working
Balanced binary tree definition
The balance factor of each node (the difference between the two subtree heights) should never exceed 1
Guarantee of O(log n) search
Balanced BST use case: B-tree, Red-black tree, AVL tree
- B-tree: paging from disk (database)
- Red-black tree: fairly frequents inserts, deletes or retrievals
- AVL tree: many retrievals, infrequent inserts and deletes
BFS and DFS tree traversal time and space complexity
BFS: time O(v), space O(v)
DFS: time O(v), space O(h) (height of the tree)
Binary tree BFS traversal
Level order traversal (level by level)
Iterative algorithm: use a queue, put the root, iterate while queue is not empty
Queue<Node> queue = new LinkedList<>();
queue.add(root);
while(!queue.isEmpty()) {
Node node = queue.poll();
visit(node);
if(node.left != null) {
queue.add(node.left);
}
if(node.right != null) {
queue.add(node.right);
}
}Binary tree definition
Tree with each node having up to two children
Binary tree DFS traversal: in-order, pre-order and post-order
- In-order: left-root-right
- Pre-order: root-left-right
- Post-order: left-right-root
It’s depth first so:
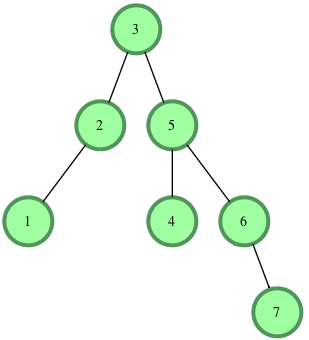
- In-order: 1, 2, 3, 4, 5, 6, 7
- Pre-order: 3, 2, 1, 5, 4, 6, 7
- Post-order: 1, 2, 4, 7, 6, 5, 3
Binary tree: complete
Every level of the tree is fully filled, with last level filled from the left to the right
Binary tree: full
Each node has 0 or 2 children
Binary tree: perfect
2^l - 1 nodes with l the level: 1, 3, 7, etc. nodes
Every level is fully filled
BST complexity: access, insert, delete
If not balanced O(n)
If balanced O(log n)
BST definition
Binary tree in which every node must fit the property: all left descendents <= n < all right descendents
Implementation: optional key, value, left, right
BST delete algo and complexity
Find inorder successor and swap it
Average: O(log n)
Worst: O(h) if not self-balanced BST, otherwise O(log n)
BST insert algo
Search for key or value (by recursively going left or right depending on the comparison) then insert a new node or reset the value (no swap)
Complexity: worst O(n)
public TreeNode insert(TreeNode root, int a) {
if (root == null) {
return new TreeNode(a);
}
if (root.val <= a) { // Left
root.left = insert(root.left, a);
} else { // Right
root.right = insert(root.right, a);
}
return root;
}BST questions prerequisite
Is it a self-balanced BST? (impacts: O(log n) time complexity guarantee)
Complexity to create a trie
Time and space: O(n * l) with n the number of words and l the longest word length
Complexity to insert a key in a trie
Time: O(k) with k the size of the key
Space: O(1) iterative, O(k) recursive
Complexity to search for a key in a trie
Time: O(k) with k the size of the key
Space: O(1) iterative or O(k) recursive
Given a binary tree, algorithm to populate an array to represent its level-by-level traversal
Solution: BFS by popping only a fixed number of elements (queue.size)
public static List<List<Integer>> traverse(TreeNode root) {
List<List<Integer>> result = new LinkedList<>();
Queue<TreeNode> queue = new LinkedList<>();
queue.add(root);
while (!queue.isEmpty()) {
List<Integer> level = new ArrayList<>();
int levelSize = queue.size();
// Pop only levelSize elements
for (int i = 0; i < levelSize; i++) {
TreeNode current = queue.poll();
level.add(current.val);
if (current.left != null) {
queue.add(current.left);
}
if (current.right != null) {
queue.add(current.right);
}
}
result.add(level);
}
return result;
}How to calculate the path number of a node while traversing using DFS?
Example: 1 -> 7 -> 3 gives 173
Solution: sum = sum * 10 + n
private int dfs(TreeNode node, int sum) {
if (node == null) {
return 0;
}
sum = 10 * sum + node.val;
// Do something
}Min (or max) value in a BST
Move recursively on the left (on the right)
Red-Black tree
Self-balanced BST => O(log n) complexity
- Root node always black
- Incoming node is red
- Red violation: child and parent are red
- Resolve violation by recoloring and/or restructuring
Further Reading
Binary Trees: Red Black by David Pynes
Red-black tree complexity: access, insert, delete
All: O(log n)
Reverse a binary tree algo
public void reverse(Node node) {
if (node == null) {
return;
}
Node temp = node.right;
node.right = node.left;
node.left = temp;
reverse(node.left);
reverse(node.right);
}Trie definition, implementation and use case
Tree-like data structure with empty root and where each node store characters
Each path down the tree represent a word (until a null node that represents the end of the word)
Usually implemented using a map of children (or a fixed size array with ASCII charset for example)
Use case: dictionnary (save memory)
Also known as prefix tree
Why to use BST over hash table
Sorted keys